#BatchNormalization ##Why

Normalization

Batch Normalization

Normalization is a widely used pre-processing trick in machine learning. The unbalanced feature scopes make learning rate hard to choose – the same learning rate may explore some features while vanish other features at the same time.

After normalization, the same learning rate imposes same effect on all features, which makes the LR easier to choose. And then make use of regularization tools to select preferred features

Internal Covariate Shift

The topic is brought up by paper: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

We define Internal Covariate Shift as the change in th distribution of network activations due to the change in network parameters during training.

An intuitive explanation is that the training of parameters of layer H_n+1 is updated based on distribution of output of H_n. But the sequence of back-propagation if from H_n+1 to H_n. So the ongoing update of different layers may conflict with each other or cancel update effect of each other.

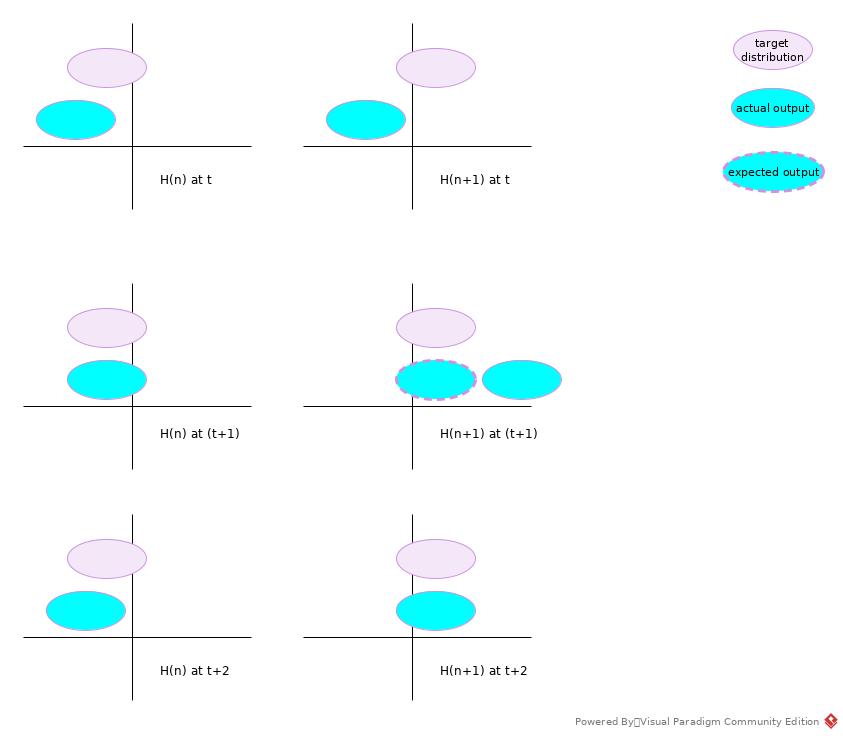
Above figure showed a simple case.

• In batch t training, H_n decided to move the output distribution to the right; H_n+1 also decided to move the distribution to the right.
• The result is that, in batch (t + 1) training, H_n output fitted the target, while H_n+1 moved too much to miss the target.
• If the learning rate is small enough, H_n+1 may move the output back to match the target, while it also pushed output of H_n away from target. So the parameters of the whole network may be updated in a zigzagged pattern.
• If the learning rate is large enough, the update would be oscillating and fail to converge.

When batch normalization has been introduced, the output the each layer would be in the fixed center with limited scope, the network just update the shape to fit into the target.

Some other papers argued that it may not the root cause of improved performance: Understanding Batch Normalization

Other Observations

• De-correlated features
• Introduced some noises as mean(batch) is not E(input)
• A Gentle Introduction to Batch Normalization for Deep Neural Networks
• Smooth How Does Batch Normalization Help Optimization?

  Algorithm

  Besides input standardization, batch-norm also introduced a linear transformation to recover representation ability of input for non-linear function in following layer. The parameters γ and β are independent of input values and learnable.

  Forward

  The *Algorithm 1* from paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.

The following sequence figure is from Batch Norm Paper Reading

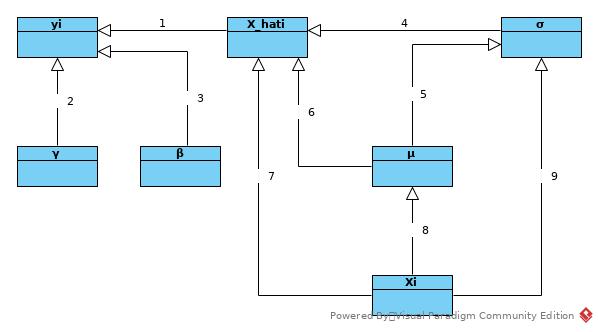
Backward

Follow the sequence shown in above figure as (reverse) topology sort.

1. ∂l/∂x_hat_i = ∂l/∂y_i * ∂y_i/∂x_hat_i = ∂l/∂y_i * γ
2. ∂l/∂γ = Σ(∂l/∂y_i * ∂y_i/∂γ) = Σ(∂l/∂y_i * x_hat_i)
3. ∂l/∂β = Σ(∂l/∂y_i * ∂y_i/∂β) = Σ(∂l/∂y_i)
4. ∂l/∂σ² = Σ(∂l/∂x_hat_i * ∂x_hat_i/∂σ²) = Σ(∂l/∂x_hat_i * (-1/2) * (x_i - μ) * (σ² + ǫ)^(-3/2))
5. ∂σ²/∂μ = (-2/m) * Σ(x_i - μ)
6. ∂x_hat_i/∂μ = (-1) * (σ2 + ε)^(-1/2)
7. ∂x_hat_i/∂x_i = (σ2 + ǫ)^(-1/2)
8. ∂μ/∂x_i = 1/m
9. ∂σ²/∂x_i = (2/m) * (x_i - μ)

Then

• ∂l/∂μ = ∂l/∂σ² * ∂σ²/∂μ + Σ(∂l/∂x_hat_i * ∂x_hat_i/∂μ)
• ∂l/∂x_i = ∂l/∂x_hat_i * ∂x_hat_i/∂x_i + ∂l/∂μ * ∂μ/∂x_i + ∂l/∂σ² * ∂σ²/∂x_i

  In Inference

  In inference, the μ and σ² are not estimation of batch input, but the E of all previous input instead.

• μ = E[μ] = mean(Σ(μ_batch))
• σ² = Var[x] = (m/(m - 1)) * mean(Σσ²_batch)

The batch-norm output is y = γ * x_hat + β = γ * ((x - μ)/(σ² + ε)^(-1/2)) + β

Benefits

• Larger learning rate
• Less sensible to parameter initiation
• Less epoch required

Notes of paper

Other References

Covariate Shift

Batch Norm(Chinese)

Batch Normalization(Andrew Ang)