GravesLSTM

Suppose there is no peephole.

Architecture

The architecture of the rnn cell is like the following figure shows:

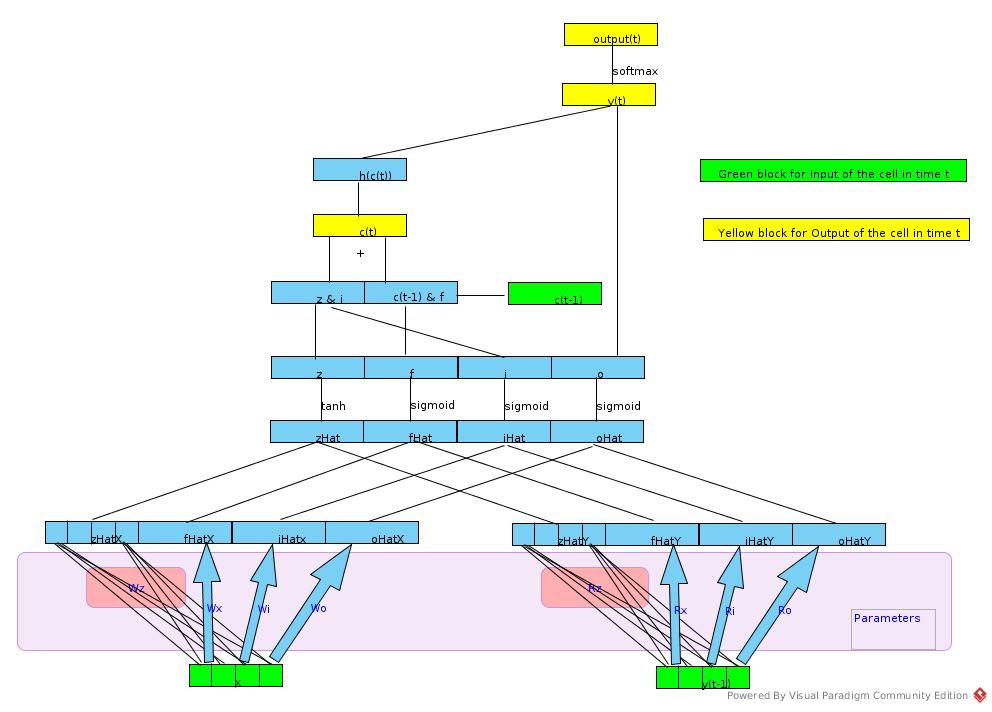
Calculation

As annotation declared in LSTMHelpers.java, this class is a implementation of this document: vector impl

The calculation is straightforward except one point. There is anothe style of calculation as demonstraed in this document: recusion impl

As declared in this document, the gradient of W/R is recursion of recursion of t, while in previous document the gradient is just recursion over t.

The point is that, the recursion in vector implementation is hidden in δ. Take lambdaWz for example:

δWz = Σ(t)(<δzHat(t), x(t)>)
δzHat(t) = δc(t) & i(t) & g'(zHat(t))
δc(t) is a function of t and (t + 1), then the same as δzHat(t).
Write δc(t) as function of t and function of (t + 1) as:
u(t) = δc(t)
v(t) = δy(t) & o(t) & h'(c(t))
u(t) = v(t) + u(t + 1) & f(t + 1)
     = v(t) + (v(t + 1) + u(t + 2) & f(t + 2)) & f(t + 1)
     = v(t) + v(t + 1) & f(t + 1) + u(t + 2) & f(t + 2) & f(t + 1)
     = v(t) + v(t + 1) & f(t + 1) + (v(t + 2) + u(t + 3) & f(t + 3)) & f(t + 2) & f(t + 1)
     = v(t) + v(t + 1) & f(t + 1) + v(t + 2) & f(t + 2) & f(t + 1) + u(t + 3) & f(t + 3) & f(t + 2) & f(t + 1)
     = v(t) + Σ(r: r = t + 1 ~ T)(v(r) & π(s: s = t + 1, r)f(s))

u(t) is in a form of summary over multiplication recursion.

That is the same as δE(t)/δW(i, j) in [Gradient for an RNN]

Forward Pass

All symbols follows that in vector impl

LSTMHelpers::activateHelper
{
        //W in form [Wz, Wf, Wi, Wo]
        INDArray inputWeights = originalInputWeights;
        // y(t - 1)
        INDArray prevOutputActivations = originalPrevOutputActivations;

        // c(t - 1)
        INDArray prevMemCellState;
        if (originalPrevMemCellState == null) {
            prevMemCellState = Nd4j.create(new int[] {miniBatchSize, hiddenLayerSize}, 'f');
        } else {
            prevMemCellState = originalPrevMemCellState.dup('f');
        }

        // R in form [Rz, Rf, Ri, Ro]
        INDArray recurrentWeightsIFOG = recurrentWeights.get(NDArrayIndex.all(), NDArrayIndex.interval(0, 4 * hiddenLayerSize)).dup('f');

        boolean sigmoidGates = gateActivationFn instanceof ActivationSigmoid;
        // Get g()
        IActivation afn = layer.layerConf().getActivationFn();
        INDArray outputActivations = null;

        for (int iTimeIndex = 0; iTimeIndex < timeSeriesLength; iTimeIndex++) {
            int time = iTimeIndex;

            //Get x
            INDArray miniBatchData = (is2dInput ? input : input.tensorAlongDimension(time, 1, 0)); //[Expected shape: [m,nIn]. Also deals with edge case of T=1, with 'time series' data of shape [m,nIn], equiv. to [m,nIn,1]
            miniBatchData = Shape.toMmulCompatible(miniBatchData);

            //ifogActivations = x * [Wz, Wf, Wo, Wi] = x * Wz, x * Wf, x * Wo, x * Wi
            INDArray ifogActivations = miniBatchData.mmul(inputWeights); //Shape: [miniBatch,4*layerSize]

            //ifogActivations += y * [Rz, Rf, Ro, Ri]
            Nd4j.gemm(prevOutputActivations, recurrentWeightsIFOG, ifogActivations, false, false, 1.0, 1.0);
            //ifogActivations += b
            ifogActivations.addiRowVector(biases);

            //zHat = inputActivations = ifogActivations[0]
            INDArray inputActivations =
                            ifogActivations.get(NDArrayIndex.all(), NDArrayIndex.interval(0, hiddenLayerSize));

            //z = inputActivations = g(inputActivations) = g(zHat)
            layer.layerConf().getActivationFn().getActivation(inputActivations, training);

            //fHat = forgetGateActivations = ifogActivations[1]
            INDArray forgetGateActivations = ifogActivations.get(NDArrayIndex.all(),
                            NDArrayIndex.interval(hiddenLayerSize, 2 * hiddenLayerSize));
            //f = forgateGateActivations = sigmoid(forgateGateActivations)
            gateActivationFn.getActivation(forgetGateActivations, training);

            //iHat = inputModGateActivations = ifogActivations[3]
            INDArray inputModGateActivations = ifogActivations.get(NDArrayIndex.all(),
                            NDArrayIndex.interval(3 * hiddenLayerSize, 4 * hiddenLayerSize));

            //i = inputModGateActivations = sigmoid(iHat)
            gateActivationFn.getActivation(inputModGateActivations, training);

            //c(t) = f & c(t - 1)
            currentMemoryCellState = forgetGateActivations.muli(prevMemCellState);
            //inputModMulInput = i & z
            inputModMulInput = inputModGateActivations.muli(inputActivations);        }

            //c(t) = c(t) + i & z = f & c(t - 1) + i & z
            l1BLAS.axpy(currentMemoryCellState.length(), 1.0, inputModMulInput, currentMemoryCellState); //currentMemoryCellState.addi(inputModMulInput)

            //oHat = outputGateActivations = ifogActivations[2]
            INDArray outputGateActivations = ifogActivations.get(NDArrayIndex.all(),
                            NDArrayIndex.interval(2 * hiddenLayerSize, 3 * hiddenLayerSize));
            //o = sigmoid(oHat)
            gateActivationFn.getActivation(outputGateActivations, training);

            //h(c(t))
            INDArray currMemoryCellActivation = afn.getActivation(currentMemoryCellState.dup('f'), training);
            //y(t) = c(t) & o
            currHiddenUnitActivations = currMemoryCellActivation.muli(outputGateActivations); //Expected shape: [m,hiddenLayerSize]
        }
}

Backward Pass

Volcabularies:

    iz = zHat
    ia = z
    fa = f
    ga = i
    oa = o

    currentMemoryCellState = c(t)
    currHiddenUnitActivations = y
    fwdPassOutputAsArrays = y
    memCellState = c(t)
    memCellActivations = h(c(t))

    epsilonNext = ∆(t + 1)
    nablaCellStateNext = δc(t + 1)
    deltaifogNext = [deltaiNext, deltafNext, deltaoNext, deltagNext]
    deltaiNext = δzHat(t)
    deltafNext = δfHat(t)
    deltaoNext = δoHat(t)
    deltagNext = δiHat(t)

    iwGradientsOut = [δWz, δWf, δWo, δWi]
    rwGradientsOut = [δRz, δRf, δRo, δRi]
    bGradientsOut = [δbz, δbf, δbo, δri]
    wIFOG = [Rz, Rf, Ro, Ri]

    nablaCellState = δc(t)
    prevMemCellState = c(t - 1)
    prevHiddenUnitActivation = y(t - 1)
    currMemCellState(t)
    epsilonSlice = ∆(t)

    nablaOut = δy(t)
    sigmahOfS = h(c(t))
    ao = oa = o
    deltao = δoHat(t)

    af = f(t)
    ag = i(t)
    ai = z(t)
    zi = zHat(t)

LSTMHelpers::activateHelper()
{
        //Initiation toReturn
        if (forBackprop) {
            toReturn.fwdPassOutputAsArrays = new INDArray[timeSeriesLength];
            toReturn.memCellState = new INDArray[timeSeriesLength];
            toReturn.memCellActivations = new INDArray[timeSeriesLength];
            toReturn.iz = new INDArray[timeSeriesLength];
            toReturn.ia = new INDArray[timeSeriesLength];
            toReturn.fa = new INDArray[timeSeriesLength];
            toReturn.oa = new INDArray[timeSeriesLength];
            toReturn.ga = new INDArray[timeSeriesLength];
        }

        for (int iTimeIndex = 0; iTimeIndex < timeSeriesLength; iTimeIndex++)
        {
            if (forBackprop) {
                // iz[time] = zHat(t)
                toReturn.iz[time] = inputActivations.dup('f');
            }

            // ia[time] = z(t)
            if (forBackprop)
                toReturn.ia[time] = inputActivations;

            // fa[time] = f(t)
            if (forBackprop)
                toReturn.fa[time] = forgetGateActivations;

            // ga[time] = i(t)
            if (forBackprop)
                toReturn.ga[time] = inputModGateActivations;
            if (forBackprop) {
                // currentMemoryCellState = c(t - 1) & f(t)
                currentMemoryCellState = prevMemCellState.dup('f').muli(forgetGateActivations);
                // inputModMulInput = z(t) & i(t)
                inputModMulInput = inputModGateActivations.dup('f').muli(inputActivations);
            }
            // currentMemoryCellState = c(t)
            l1BLAS.axpy(currentMemoryCellState.length(), 1.0, inputModMulInput, currentMemoryCellState); //currentMemoryCellState.addi(inputModMulInput)


            // oa[time] = o(t)
            if (forBackprop)
                toReturn.oa[time] = outputGateActivations;

            if (forBackprop) {
                // currHiddenUnitActivations = y(t)
                currHiddenUnitActivations = currMemoryCellActivation.dup('f').muli(outputGateActivations); //Expected shape: [m,hiddenLayerSize]
            }

            if (forBackprop) {
                // fwdPassOutputAsArrays[time] = y(t)
                toReturn.fwdPassOutputAsArrays[time] = currHiddenUnitActivations;
                //memCellState[time] = c(t)
                toReturn.memCellState[time] = currentMemoryCellState;
                //memCellActivations = h(c(t))
                toReturn.memCellActivations[time] = currMemoryCellActivation;
            }

        }

}

toReturn in in activateHelper passed into backpropGradientHelper as fwdPass

LSTMHelper::backpropGradientHelper()
{
        // Get wIFOG = [Rz, Rf, Ro, Ri]
        INDArray wIFOG = recurrentWeights.get(NDArrayIndex.all(), NDArrayIndex.interval(0, 4 * hiddenLayerSize));

        //Initialization
        // ∆(t)
        INDArray epsilonNext = Nd4j.create(new int[] {miniBatchSize, prevLayerSize, timeSeriesLength}, 'f'); //i.e., what would be W^L*(delta^L)^T. Shape: [m,n^(L-1),T]
        // δc(t + 1) = nablaCellStateNext
        INDArray nablaCellStateNext = null;
        // deltaifogNext = [δzHat(t), δfHat(t), δoHat(t), δiHat(t)]
        INDArray deltaifogNext = Nd4j.create(new int[] {miniBatchSize, 4 * hiddenLayerSize}, 'f');
        INDArray deltaiNext = deltaifogNext.get(NDArrayIndex.all(), NDArrayIndex.interval(0, hiddenLayerSize));
        INDArray deltafNext = deltaifogNext.get(NDArrayIndex.all(),
                        NDArrayIndex.interval(hiddenLayerSize, 2 * hiddenLayerSize));
        INDArray deltaoNext = deltaifogNext.get(NDArrayIndex.all(),
                        NDArrayIndex.interval(2 * hiddenLayerSize, 3 * hiddenLayerSize));
        INDArray deltagNext = deltaifogNext.get(NDArrayIndex.all(),
                        NDArrayIndex.interval(3 * hiddenLayerSize, 4 * hiddenLayerSize));

        // Initialize δW(t), δR(t), δb(t)
        INDArray iwGradientsOut = gradientViews.get(inputWeightKey);
        INDArray rwGradientsOut = gradientViews.get(recurrentWeightKey); //Order: {I,F,O,G,FF,OO,GG}
        INDArray bGradientsOut = gradientViews.get(biasWeightKey);

        for (int iTimeIndex = timeSeriesLength - 1; iTimeIndex >= endIdx; iTimeIndex--) {
        {
            int time = iTimeIndex;
            int inext = 1;

            // Initialize
            // nablaCellState = δc(t)
            nablaCellState = Nd4j.create(new int[] {miniBatchSize, hiddenLayerSize}, 'f');

            // prevMemCellState = c(t - 1)
            INDArray prevMemCellState = (iTimeIndex == 0 ? fwdPass.prevMemCell : fwdPass.memCellState[time - inext]);
            // preHiddenUnitActivations = y(t - 1)
            INDArray prevHiddenUnitActivation =
                            (iTimeIndex == 0 ? fwdPass.prevAct : fwdPass.fwdPassOutputAsArrays[time - inext]);
            // c(t)
            INDArray currMemCellState = fwdPass.memCellState[time];

            // ∆(t)
            INDArray epsilonSlice = (is2dInput ? epsilon : epsilon.tensorAlongDimension(time, 1, 0)); //(w^{L+1}*(delta^{(L+1)t})^T)^T or equiv.

            // nablaOut = δy(t) = ∆(t)
            INDArray nablaOut = Shape.toOffsetZeroCopy(epsilonSlice, 'f'); //Shape: [m,n^L]
            if (iTimeIndex != timeSeriesLength - 1) {
                // deltaifogNext is function of (t + 1) from previous loop
                // δy(t) = ∆(t) + Rz * δzHat(t + 1) + Rf * δfHat(t + 1) + Ro * δoHat(t + 1) + Ri * δiHat(t + 1)
                Nd4j.gemm(deltaifogNext, wIFOG, nablaOut, false, true, 1.0, 1.0);
            }

            // sigmahOfS = h(c(t))
            INDArray sigmahOfS = fwdPass.memCellActivations[time];
            // ao = o(t)
            INDArray ao = fwdPass.oa[time];

            // deltao = δoHat(t)
            INDArray deltao = deltaoNext;
            // deltao = δoHat(t) = h(c(t)) & δy(t)
            Nd4j.getExecutioner().exec(new OldMulOp(nablaOut, sigmahOfS, deltao));
            if (sigmoidGates) {
                // sigmaoPrimeOfZo = σ'(oHat(t))
                INDArray sigmaoPrimeOfZo = Nd4j.getExecutioner().execAndReturn(new TimesOneMinus(ao.dup('f'))); //Equivalent to sigmoid deriv on zo
                // deltao = δoHat(t) = h(c(t)) & δy(t) & σ'(oHat(t))
                deltao.muli(sigmaoPrimeOfZo);
            }

            //Memory cell error:
            // temp = h'(c(t)) & o(t) & δy(t)
            INDArray temp = afn.backprop(currMemCellState.dup('f'), ao.muli(nablaOut)).getFirst(); //TODO activation functions with params
            // δc(t) += temp = h'(c(t)) & o(t) & δy(t)
            l1BLAS.axpy(nablaCellState.length(), 1.0, temp, nablaCellState);
            if (iTimeIndex != timeSeriesLength - 1) {
                // nextForgetGatesAs = f(t + 1)
                INDArray nextForgetGateAs = fwdPass.fa[time + inext];
                int length = nablaCellState.length();
                // nablaCellState += f(t + 1) & δc(t + 1)
                // δc(t) += f(t + 1) & δc(t + 1)
                l1BLAS.axpy(length, 1.0, nextForgetGateAs.muli(nablaCellStateNext), nablaCellState); //nablaCellState.addi(nextForgetGateAs.mul(nablaCellStateNext))
            }

            // δc(t + 1) = δc(t)
            nablaCellStateNext = workspace == null ? nablaCellState : nablaCellState.leverage();


            // af = f(t)
            INDArray af = fwdPass.fa[time];
            INDArray deltaf = null;
            if (iTimeIndex > 0 || prevMemCellState != null) { //For time == 0 && no prevMemCellState, equivalent to muli by 0
                //Note that prevMemCellState may be non-null at t=0 for TBPTT
                deltaf = deltafNext;
                if (sigmoidGates) {
                    // deltafNext = deltaf = σ'(fHat(t))
                    Nd4j.getExecutioner().exec(new TimesOneMinus(af, deltaf));
                    // deltafNext = deltaf & δc(t)
                    deltaf.muli(nablaCellState);
                    // δfHat(t) = deltafNext = deltaf & c(t - 1) = σ'(fHat(t)) & δc(t) & c(t - 1)
                    deltaf.muli(prevMemCellState);
                }
            }

            // ag = i
            INDArray ag = fwdPass.ga[time];
            // ai = z(t)
            INDArray ai = fwdPass.ia[time];
            INDArray deltag = deltagNext;
            if (sigmoidGates) {
                // deltag = deltagNext = σ'(iHat(t))
                Nd4j.getExecutioner().exec(new TimesOneMinus(ag, deltag)); //Equivalent to sigmoid deriv on zg
                //deltagNext = deltaNext & z(t)
                deltag.muli(ai);
                //δiHat(t) = deltagNext = σ'(iHat(t)) & z(t) & δc(t)
                deltag.muli(nablaCellState);
            }

            // zi = zHat(t)
            INDArray zi = fwdPass.iz[time];
            INDArray deltai = deltaiNext;
            // temp = δc(t) & i(t)
            temp = Nd4j.getExecutioner().execAndReturn(
                            new OldMulOp(ag, nablaCellState, Nd4j.createUninitialized(deltai.shape(), 'f')));
            // δzHat(t) = g'(zHat(t)) & δc(t) & i(t)
            deltai.assign(afn.backprop(zi, temp).getFirst());

            // iwGradientsOut = [δWz, δWf, δWo, δWi]
            // prevLayerActivationSlice = x(t)
            INDArray prevLayerActivationSlice =
                            Shape.toMmulCompatible(is2dInput ? input : input.tensorAlongDimension(time, 1, 0));
            if (iTimeIndex > 0 || prevHiddenUnitActivation != null) { //For time == 0 && no prevMemCellState, equivalent to muli by 0
                //Note that prevHiddenUnitActivations may be non-null at t=0 for TBPTT
                //Again, deltaifog_current == deltaifogNext at this point... same array
                // iwGradientsOut = x * [δzHat, δfHat, δoHat, δiHat]
                Nd4j.gemm(prevLayerActivationSlice, deltaifogNext, iwGradientsOut, true, false, 1.0, 1.0);
            } else {
                // iwGradientsOut = [δzHat(t) * x, ?, δoHat(t) * x, δiHat(t) * x]
                // As fHat part requires (t + 1) component
                INDArray iwGradients_i =
                                iwGradientsOut.get(NDArrayIndex.all(), NDArrayIndex.interval(0, hiddenLayerSize));
                Nd4j.gemm(prevLayerActivationSlice, deltai, iwGradients_i, true, false, 1.0, 1.0);
                INDArray iwGradients_og = iwGradientsOut.get(NDArrayIndex.all(),
                                NDArrayIndex.interval(2 * hiddenLayerSize, 4 * hiddenLayerSize));
                INDArray deltaog = deltaifogNext.get(NDArrayIndex.all(),
                                NDArrayIndex.interval(2 * hiddenLayerSize, 4 * hiddenLayerSize));
                Nd4j.gemm(prevLayerActivationSlice, deltaog, iwGradients_og, true, false, 1.0, 1.0);
            }

            // rwGradientsIFOG = [δRz, δRf, δRo, δRi]
            if (iTimeIndex > 0 || prevHiddenUnitActivation != null) {
                //If t==0 and prevHiddenUnitActivation==null, equiv. to zeros(n^L,n^L), so dL/dW for recurrent weights
                // will end up as 0 anyway
                //At this point: deltaifog and deltaifogNext are the same thing...
                //So what we are actually doing here is sum of (prevAct^transpose * deltaifog_current)
                // [δRz, δRf, δRo, δRi] = [y(t - 1) * δzHat(t), y(t - 1) * δfHat(t), y(t - 1) * δoHat(t), y(t - 1) * δiHat(t)]
                Nd4j.gemm(prevHiddenUnitActivation, deltaifogNext, rwGradientsIFOG, true, false, 1.0, 1.0);
            }

            // δx(t) = Wz * δzHat(t) + Wf * δfHat(t) + Wo * δoHat(t) + Wi * δiHat(t)
            INDArray epsilonNextSlice = epsilonNext.tensorAlongDimension(time, 1, 0); //This slice: f order and contiguous, due to epsilonNext being defined as f order.
            if (iTimeIndex > 0 || prevHiddenUnitActivation != null) {
                 //Note that prevHiddenUnitActivation may be non-null at t=0 for TBPTT
                 // δx(t) = Wz * δzHat(t) + Wf * δfHat(t) + Wo * δoHat(t) + Wi * δiHat(t)
                 Nd4j.gemm(deltaifogNext, inputWeights, epsilonNextSlice, false, true, 1.0, 1.0);
             } else {
                 // Similar to W, without fHat part
                 //No contribution from forget gate at t=0
                 INDArray wi = inputWeights.get(NDArrayIndex.all(), NDArrayIndex.interval(0, hiddenLayerSize));
                 Nd4j.gemm(deltai, wi, epsilonNextSlice, false, true, 1.0, 1.0);
                 INDArray deltaog = deltaifogNext.get(NDArrayIndex.all(),
                                 NDArrayIndex.interval(2 * hiddenLayerSize, 4 * hiddenLayerSize));
                 INDArray wog = inputWeights.get(NDArrayIndex.all(),
                                 NDArrayIndex.interval(2 * hiddenLayerSize, 4 * hiddenLayerSize));
                 Nd4j.gemm(deltaog, wog, epsilonNextSlice, false, true, 1.0, 1.0); //epsilonNextSlice.addi(deltao.mmul(woTranspose)).addi(deltag.mmul(wgTranspose));
             }
        }
}