Chapter12

∑ τ α π δ γ ∏ Δ Λ μ ∈ ∀ β λ ∞

References

towardsdatascience

Alister Reis’s blog

MIT ppt

Maybe Coursera

True TD Lambda

Exercises

12.1

G_t:t+n = R_t+1 + γR_t+2 + … + γⁿv(S_t+n, w_t+n-1)

= R_t+1 + γ(R_t+1+1 + … + γ^n-1v(S_(t+1)+(n-1), w_{(t+1)+(n-1)-1}))

= R_t+1 + γG_t+1:t+1+n-1

G_t:t+1 = R_t+1 + γv(S_t+1, w_t)

G_t+1:t+1 = v(S_t+1, w_t)

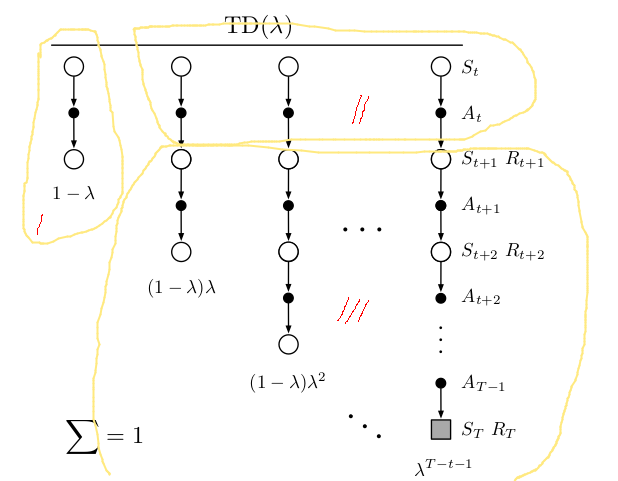
G_t^λ = (1 - λ)∑_n=(1,∞)λ^n-1G_t:t+n

= (1 - λ)∑_n=(1,∞)λ^n-1(R_t+1 + γG_t+1:t+1+n-1)

= (1 - λ)(∑_n=(1,∞)λ^n-1R_t+1 + γλ^1-1G_t+1:t+1 + λ∑_n=(1,∞)γG_t+1:t+1+n)

= R_t+1 + (1 - λ)γv(S_t+1, w_t) + γλG_t+1

12.2

(1 - λ)λ^τ = (1 - λ) / 2

λ^τ = 1 /2

τ = log_λ(1/2)

12.3

1. w_t+1 = w_t + α[G_t^λ - v(S_t,w_t)]dv(S_t,w_t)

2. δ_t = R_t+1 + γv(S_t+1,w_t) - v(S_t,w_t)

3. G_t^λ = R_t+1 + (1 - λ)γv(S_t+1, w_t) + γλG_t+1

4. G_t - V(S_t) = ∑_k=t:T-1γ^k-tδ_k

G_t - V(S_t) = R_t+1 + (1 - λ)γv(S_t+1, w_t) + γλG_t+1 - V(S_t) …(3)

= R_t+1 + γv(S_t+1,w_t) - v(S_t,w_t) - λγv(S_t+1,w) + λγG_t+1^λ

= δ_t + λγ(G_t+1^λ - v(S_t+1,w_t)) …(2)

= δ_t + λγ(δ_t + λγ(G_t+2^λ - v(S_t+2,w_t)))

= ∑_k=t:∞(λγ)^k-tδ_k

12.4

∑ τ α π δ γ ∏ Δ Λ μ ∈ ∀ β λ ∞

TD(λ):

Δw = α∑_tδ_tz_t

z_t+1 = γλz_t + dV(S_t,w)

z_t+2 = γλz_t+1 + dV(S_t+1,w)

= γλ(γλz_t + dV(S_t,w)) + dV(S_t+1,w)

= γλ²z_t + γλz_t+1 + z_t+2

z_t+n = ∑_k=0:n(γλ)^n-kdV(S_t+k)

Δw = α∑_tδ_t∑_k=0:t(γλ)^t-kdV(S_k)

Don’t know how to prove it, refer to LyWangPx

12.5

(1) G_t:h - G_t:h-1

= δ_t + V_t + γ(G_t+1:t+n - V_t+1) - δ_t - V_t - γ(G_t+1:t+n-1 - V_t+1)

= γ(G_t+1:t+n - G_t+1:t+n-1)

= …

= γⁿ(G_t+n-1:t+n - G_t+n-1:t+n-1)

= γⁿ(R_t+n + γV_t+n - V_t)

= γ^hδ_t+h

(2) ∑_n=1:h-t-1λ^n-1G_t:t+n - λ∑_n=1:h-t-2λ^n-1G_t:t+n

= ∑_n=1:h-t-2λ^n-1(G_t:t+n - λ*λ^n-1G_t:t+n) + λ^h-t-2G_t:t+h-t-1

= (1 - λ)∑_n=1:h-t-2λ^n-1G_t:t+n + λ^h-t-2G_t:h-1

(3) G_t:h^λ = (1 - λ)∑_n=1:h-t-1λ^n-1G_t:t+n + λ^h-t-1G_t:h

= ∑_n=1:h-t-1λ^n-1G_t:t+n - λ∑_n=1:h-t-1λ^n-1G_t:t+n + λ^h-t-1G_t:h

= ∑_n=1:h-t-1λ^n-1G_t:t+n - λ∑_n=1:h-t-2λ^n-1G_t:t+n - λ^h-t-1G_t:h-1 + λ^h-t-1G_t:h

= (1 - λ)∑_n=1:h-t-2λ^n-1G_t:t+n + λ^h-t-2G_t:h-1 + λ^h-t-1γ^hδ_t+h

= Solve it recursively

(4) Intuitively, G_t+1 - G_t = estimated δ decayed by γ and λ

12.6

    Loop for i in F(S,A):
        δ -= wi
        zi += 1
    ...
    Loop for i in F(S',A): δ += γwi
    w += αδz
    z = (1-α)γλz
    S = S'; A = A'

12.6

G_t^λ_s = (1-λ_t+1)G_t + γ_t+1λ_t+1G_t+1^λ_s + λ_t+1R_t+1

Part I: λ_t+1R_t+1

Part II: (1-λ_t+1)G_t

Part III: γ_t+1λ_t+1G_t+1^λ_s

G_t^λ_s = R_t+1 + γ_t+1((1-λ_t+1)v(S_t+1,w_t) + λ_t+1G_t+1^λ_s)

Gt:hλs = Rt+1 + γt+1((1-λt+1)v(St+1,wt) + λt+1Gλst+1:h)

Gt:hλa = Rt+1 + γt+1((1-λt+1)q(St+1,At+1,wt) + λt+1Gλat+1:h)

Gt:hλs = Rt+1 + γt+1((1-λt+1)vexp(St+1) + λt+1Gλst+1:h)