#Chapter04

4.1

q_π(s,a) = ∑_s’p(s’|s,a) * [r + γ * v_π(s’)]

p(s’	s,a) = 1, r = -1, γ = 1

q_π(11, down) = -1 + v(T)

q_π(7, down) = -1 + v(11)

4.2

|S|1|2|3| |—|—|—|—| |4|5|6|7| |8|9|10|11| |12|13|14|T| |X|15|X|X|

v(s) = ∑aπ(a

s) ∑s’p(s’

s,a)[r + γ * vπ(s’)]

π(a

s) = 1/4, p(s’

s,a) = 1, r = -1, γ = 1

v(15) = 1/4 * [(-1 + v(12)) + (-1 + v(13)) + (-1 + v(14)) + (-1 + v(15))]

= -1 + [v(12) + v(13) + v(14) + v(15)] / 4

v(13) = -1 + [v(9) + v(12) + v(14) + v(15)] / 4

Solve equations:

v(13) = -20, v(15) = -20

4.3

q_π(s,a) = E_π[R + γG’ | s,a]

= Eπ[R + γv(s’)

s,a]

= Eπ[R + γ∑a’π(a’

s’) * qπ(s’,a’)

s,a]

= ∑_s’p(s’|s,a) * [R + γ∑_a’π(a’|s’) * q_π(s’,a’)]

4.4

• Set threshold for steps updated per state/per evaluation, no update when threshold reached
• Set threshold for state value, no update when threshold reached
• Set γ < 1
• Check policy to detect negative infinite loop

  4.5

  codes

  4.6

  1.  Initiation
  Initialize Q(s,a) ∀{s,a | s∈S,a∈A}; initialize π(s) ∀s∈S
  2. Policy Evaluation
  Repeat
    ∆ <- 0
    for each (s,a) ∈ SxA:
      q <- Q(s,a)
      Q(s,a) <- ∑(s')p(s'|s,a) * [R + γ∑(a')π(a'|s') * q[π](s',a')]
      ∆ <- max(∆, |Q(s,a) - q|)
  until ∆ < θ
  3. Policy Improvement
   policy-stable <- true
   For each s ∈ S:
     a <- π(s)
     π(s) <- argmax(a)Q(s,a)
     if a != π(s):
        then policy-stable = false
   if policy-stable:
     then stop
   else:
     goto 2
  

  4.7

  Step1

  Initialize π(s) = ϵ * u(s) + (1 - ϵ) * A / |A|, u(s) = original π(s) in figure 4.3

  Step2

  V(s) = ϵ * ∑_s’p(s’|s,a)[r + γ * V_u(s’)] + (1 - ϵ) / |A| * ∑_a∑_s’p(s’|s,a) * [r + γ * V(s’)]

  Step3

  u(s) = argmax_a∑_s’p(s’|s,a) * [r + γv(s’)]

  4.8

  Seemed that the original implementation breaks tie by order. That is, the algorithm is looking for most rewarded, and the fastest solution at the same time.

So in s = 50, action = 50 get the best value as it has chance to win in 1 step with possibility = PH. Similarly, in s = 25, action = 25 get the best value. While as the 25 % 2 == 1, there is no similar spike in s = 12/13.

Then for s = 51, the best choice is to bet 1. In winning case, the player get positive reward; in lost case, the player reach s = 50, a good state. For s = 52, 53, …, the V(s) is looking for balance between going back to s = 50 with negative reward and going forward to relative better states.

ref1

ref2

4.9

codes

Figure for ph = 0.25

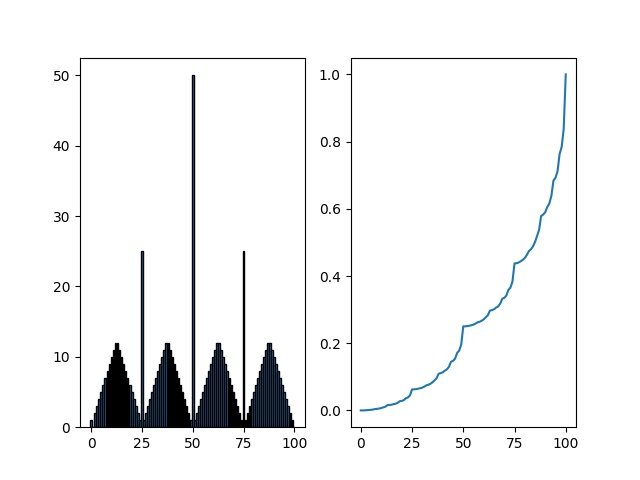
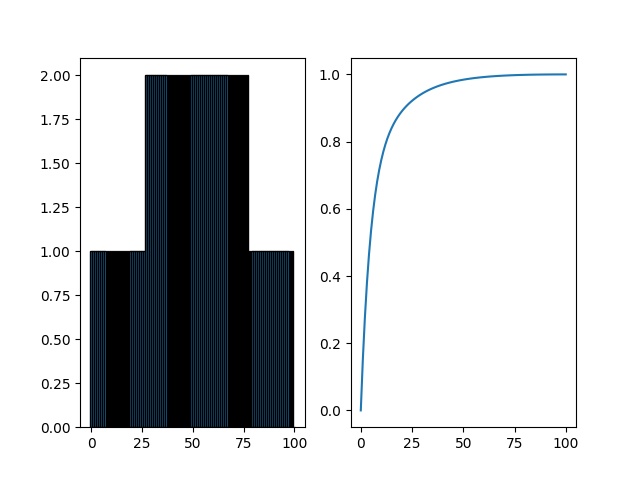
Figure for ph = 0.55

4.10

q(s,a) = ∑_s’p(s’|s,a) * [r + γmax_a’q(s’,a’)]